C++을 통한 오디오 파일의 DFT와 IDFT 처리 - 진행중

꽤 긴 글이될 것 같아서 일단 미리 정리하고 한다.

일단 이번에 하는 것은 미니 프로젝트 개념이다.

 

오디오 파일을 읽어와서 샘플링 하고 

이 값을 DFT로 처리하고, IDFT로 다시 돌린 값을

csv 파일 형식으로 저장하는 C++ 프로그램을 짜는 것이 목표다.

 

지난 면접에서 디지털 설계에는 디지털 필터 설계가 있다는 것을 배우고

이를 위해서 z 변환을 사용한다고 들었다.

이를 위한 기초로 푸리에 변환과 라플라스 변환을 배우는 

신호 및 시스템 내용을 복습하고 있다.

 

이번에는 C++을 활용해서 DFT 함수와 IDFT 함수를 구현해볼 계획이다.

정확히는 모르지만, 결국 디지털 필터를 설계하면 결과가 정확한지 비교하는

레퍼런스 모델이 필요하고 비교용으로 만드는 것 같다.

 

 

일단 어떤 느낌으로 작성하는지 찾아보려다가 

https://stackoverflow.com/questions/51679516/discrete-fourier-transform-c

Discrete Fourier Transform C++

여기에서 아주 기초적으로 구현한 C++ 코드를 발견했다.

일단 DFT이고

complex<double> DFT(double in, int k)
{
    double a = 0;
    double b = 0;
    int N = input.size();
    for(int n = 0; n < N; n++)
    {
        a+= cos((2 * M_PI * k * n) / N) * input[n];
        b+= -sin((2 * M_PI * k * n) / N) * input[n];
    }
    complex<double> temp(a, b);
    return temp;
}

이건 IDFT이다. 

double IDFT(size_t n)
{
    double a = 0;
    size_t N = output.size();
    for (size_t k = 0; k < N; k++)
    {
        auto phase = (2 * M_PI * k * n) / N;
        a += cos(phase) * output[k].real() - sin(phase) * output[k].imag();
    }
    a /= N;
    return a;
}

질문자와 답변자가 서로 다른 사람이라 코드 스타일과 문법이 조금씩 다르다.

 

이산 푸리에 변환의 기본적인 공식은 다음과 같은데

 

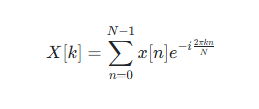
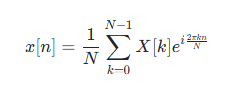
여기서 오일러 공식을 적용해서 극한값 e를 밑으로 하는 지수함수를

실수부와 허수부로 나누고 각각 코사인과 사인으로 교체해서 계산한다.

여기서는 이 공식에 충실하게 작성했다.

다만 이러면 느리다. 그래서 다른 사람이 추천한 라이브러리는 

https://www.fftw.org/

FFTW Home Page

https://sourceforge.net/projects/kissfft/

Kiss FFT

이런 라이브러리를 추천해줬다.

여기에는 추가적인 fft가 있다.

https://dsp.stackexchange.com/questions/24375/fastest-implementation-of-fft-in-c

Fastest implementation of fft in C++?

이런 것은 있기는 한데 내부 코드가 좀 더 복잡하기도 하고 주로 FFT를 통해서 연산하니 일단 업무에서는 이런 것을 쓴다는 정도로만 알자.

 

일단 메인 알고리즘은 확인했으니,

원하는 입력과 원하는 출력을 만들면 된다.

 

2024.10.07

일단 csv 출력을 위한 C++ 라이브러리를 찾았다.

 

https://github.com/d99kris/rapidcsv?tab=readme-ov-file

GitHub - d99kris/rapidcsv: C++ CSV parser library

 

입력은 고민중인데, 파일을 입력할지,

아니면 그냥 사인 신호를 몇번 샘플링 할지 결정해야겠다.

사인신호 샘플링이면, 기본 내장 라이브러리로 해결 될 것 같고,

오디오 파일이면 좀 더 찾아보자.

그냥 사인 신호 샘플링으로 생각해보자.

 

2024.10.10

조금 여유가 생겨서 정리해 둔 것을 찾아보고 있다.

일단 위의 rapidcsv는 읽어보니 읽어와서 파싱하는 쪽이라서 쓸 수는 있는데, 좀 그래서

C++로 csv 작성하는 법을 보니 fstream으로 직접 쓰는 것을 추천한다. 

그래서 이 부분은 내가 만들어보기로 했다.

 

일단, 사인 신호를 샘플링 하는 부분은 만들었다.

코드 전체 구조는

1. 사인 신호 샘플링 주파수 입력

2. 사인 신호 샘플링

3. DFT 후 따로 저장

4. IDFT후 따로 저장

5. csv로 출력 및 원본과 비교 후 그래프 플롯

으로 하기로 결정했다.

일단 1,2는 했고, 3,4는 진행중이다.

5번의 경우는 그래프 라이브러리를 찾아봤는데,

https://m.blog.naver.com/kimyu1117/222608468974

C++ 그래프(graph) 라이브러리 (GNUPlot, CvPlot) 사용하기

GNU plot과 CvPlot정도 있다.

문제는 GNU plot은 별도의 프로그램이라 cmd로 실행해야 되서 다른 사람이 만들어둔 api를 이용해야 되는데 14년 전에 대학원생분이 만드신 것이라 멀쩡한지 모르겠다.

 

CvPlot은 OpenCV 추가 라이브러리로 OpenCV 명령어로 그래프를 플롯할 수 있다고 한다.

다만 이것도 개인이 만든 라이브러리라 잘 모른다.

 

고민했는데, GNU plot이 csv 파일을 읽어서 표현해주다 보니

어차피 파일 만들어야 되는 것인데 이걸 쓰는 것이 나아보인다.

일단은 좀 더 확인하고 만들어보자.

 

 

2024.10.14

오늘 마무리 짓자.

몇군데 사이트를 참조하여 코드를 수정했다.

https://www.nayuki.io/page/how-to-implement-the-discrete-fourier-transform

How to implement the discrete Fourier transform

 

vector<complex<double> > computeDFT(const vector<complex<double> >& input) 
{
    vector<complex<double> > output;
    size_t n = input.size();
    for (size_t k = 0; k < n; k++) {  // For each output element
        complex<double> sum(0, 0);
        for (size_t t = 0; t < n; t++) {  // For each input element
            double angle = 2 * M_PI * t * k / n;
            sum += input[t] * exp(complex<double>(0, -angle));
        }
        output.push_back(sum);
    }
    return output;
}

일단 이게 DFT 코드다.

이전 코드는 지수 함수를 오일러 공식을 통해 사인과 코사인으로 나눠서 계산했으나,

이번에는 exp함수를 통해서 계산한다. 나머지는 공식 그대로 적용했다.

다만, 이제 원래는 샘플링 개수를 선택해야 하는데, 여기서는 원본 신호와 동일한 사이즈로 샘플링 했다.

 

vector<complex<double> > computeIDFT(const vector<complex<double> >& input)
{
    vector<complex<double> > output;
    size_t n = input.size();
    for (size_t k = 0; k < n; k++) {  // For each output element
        complex<double> sum(0, 0);
        for (size_t t = 0; t < n; t++) {  // For each input element
            double angle = 2 * M_PI * t * k / n;
            sum += input[t] * exp(complex<double>(0, angle));// Note the positive angle
            sum /= static_cast<double> (n);
        }
        output.push_back(sum/ static_cast<double>(n));// Divide by n
    }
    return output;
}

이번 코드는 IDFT 코드다. DFT 코드만 존재하다보니 이 부분은 내가 살짝 수정했다.

DFT 코드를 기반으로 지수함수의 계수만 살짝 바꾸고 크기를 샘플링 크기로 나눈 것이다.

 

이후 전체 코드는 다음과 같다.

#define _USE_MATH_DEFINES

#include <iostream>
#include <vector>
#include <complex>
#include <math.h>
#include "rapidcsv.h"

using namespace std;

vector<complex<double> > computeDFT(const vector<complex<double> >& input) 
{
    vector<complex<double> > output;
    size_t n = input.size();
    for (size_t k = 0; k < n; k++) {  // For each output element
        complex<double> sum(0, 0);
        for (size_t t = 0; t < n; t++) {  // For each input element
            double angle = 2 * M_PI * t * k / n;
            sum += input[t] * exp(complex<double>(0, -angle));
        }
        output.push_back(sum);
    }
    return output;
}

vector<complex<double> > computeIDFT(const vector<complex<double> >& input)
{
    vector<complex<double> > output;
    size_t n = input.size();
    for (size_t k = 0; k < n; k++) {  // For each output element
        complex<double> sum(0, 0);
        for (size_t t = 0; t < n; t++) {  // For each input element
            double angle = 2 * M_PI * t * k / n;
            sum += input[t] * exp(complex<double>(0, angle));// Note the positive angle
        }
        output.push_back(sum/ static_cast<double>(n));// Divide by n
    }
    return output;
}

int main()
{
    int Sample_rate = 192;
    cout << "Sample rate : ";
    cin >> Sample_rate;
    cout << "Sample rate is " << Sample_rate <<"Hz" << endl;

    vector<complex<double>> sin_sampling;

    for (int i = 0; i < Sample_rate; i++)
    {
        sin_sampling.push_back(sin(2 * M_PI / Sample_rate * i));
    }

    vector<complex<double>> signal_dft = computeDFT(sin_sampling);
    vector<complex<double>> signal_idft = computeIDFT(signal_dft);
    cout << "result" << endl;
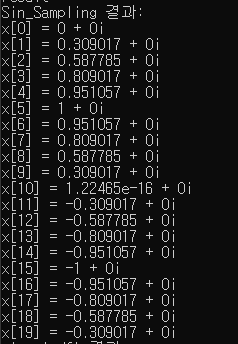
    std::cout << "Sin_Sampling 결과:" << std::endl;
    for (int i = 0; i < Sample_rate; i++) {
        std::cout << "x[" << i << "] = " << sin_sampling[i].real() << " + " << sin_sampling[i].imag() << "i" << std::endl;
    }
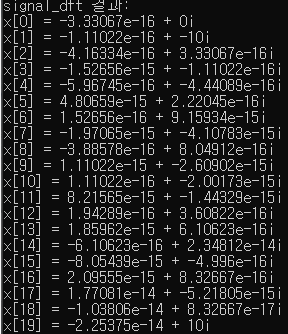
    std::cout << "signal_dft 결과:" << std::endl;
    for (int i = 0; i < Sample_rate; i++) {
        std::cout << "x[" << i << "] = " << signal_dft[i].real() << " + " << signal_dft[i].imag() << "i" << std::endl;
    }
    std::cout << "signal_idft 결과:" << std::endl;
    for (int i = 0; i < Sample_rate; i++) {
        std::cout << "x[" << i << "] = " << signal_idft[i].real() <<  std::endl;
    }
}

 

연산 결과 다시 원본 신호로 돌아온 것을 확인할 수 있다.

다만 구간이 작아서 주기함수로 나왔는지는 확인할 수 없었다.

그리고 idft 결과는 실수 부분은 돌아왔으나, 원본에 없던 허수 부분이 붙었다.

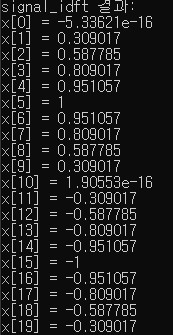
이제 추가할 부분은 파일 입출력과 출력을 csv로 출력하는 것이다.